이분 매칭
Updated:
Categories: Algorithm Theory
이분매칭이란?
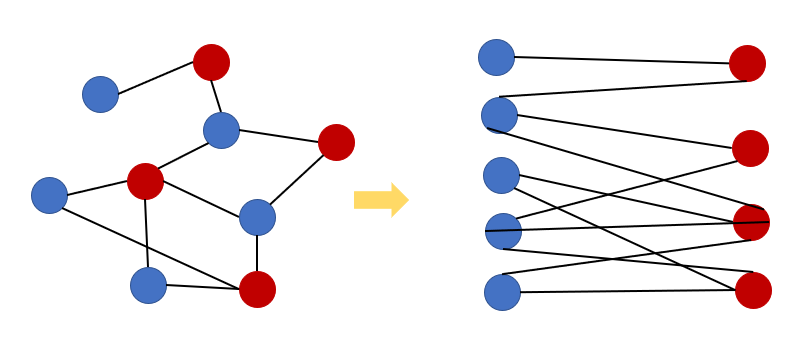 위 그림과 같이 인접한 정점끼리 서로 다른 색으로 색칠하는데 모든 정점을 2가지 색으로만 표현할 수 있으면 이를
위 그림과 같이 인접한 정점끼리 서로 다른 색으로 색칠하는데 모든 정점을 2가지 색으로만 표현할 수 있으면 이를 이분 그래프라고 한다.
이분매칭은 이러한 이분 그래프에서 각 정점이 최대 1개의 간선만 갖을 수 있으면서 그러한 간선(매칭)을 최대로 하는 기법이다.
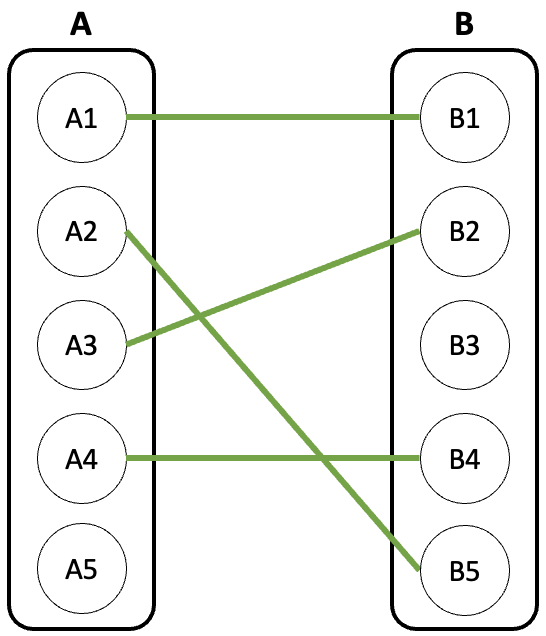
시간복잡도
dfs로 구현하면 O(VE)이다.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class BipartiteMatching {
private:
int ln, rn; // (1~ln) -> (1~rn) bipartite graph
vector<vector<int>> g; // g[1~ln]
vector<bool> visited; // visited[1~ln]
vector<int> parent; // parent[1~rn]
public:
BipartiteMatching() {}
BipartiteMatching(int _ln, int _rn) : ln(_ln), rn(_rn), g(_ln+1), visited(_ln+1), parent(_rn+1) {}
~BipartiteMatching() { this->clear(); }
void clear() {
for(int i=1; i<=ln; i++) g[i].clear();
}
void add_edge(int u, int v) { g[u].emplace_back(v); }
bool dfs(int here) {
// 이미 처리한 노드는 더 이상 볼 필요가 없음
if(visited[here]) return false;
visited[here] = true;
// 연결된 모든 노드에 대해서 들어갈 수 있는지 시도
for(int there : g[here]) {
if(parent[there] == -1 || dfs(parent[there])) {
parent[there] = here;
return true;
}
}
return false;
}
int matching() {
fill(all(parent), -1);
int ret = 0;
for(int i=1; i<=ln; i++) {
fill(all(visited), false);
ret += dfs(i);
}
return ret;
}
};
참고
https://blog.naver.com/ndb796/221240613074 https://gmlwjd9405.github.io/2018/08/23/algorithm-bipartite-graph.html
이분매칭의 활용
최소 버텍스 커버 (Minimum Vertex Cover)
버텍스 커버란, 정점 집합 S가 있을 때, 모든 간선은 양 끝점 중 적어도 하나가 S에 포함되어 있어야 한다.
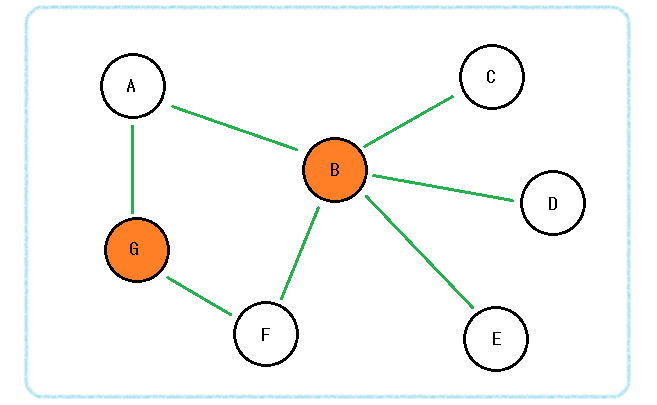
이떄 최소 버텍스 커버는 집합 S의 크기가 최소가 될 때의 그 크기를 말한다.
아래 그림의 주황색 노드가 S가 되면 그래프는 버텍스 커버가 된다.
쾨니그 정리 (Konig’s Theorem)
쾨니그의 정리에 따르면, 아래가 성립한다.
\[|Minimun \,Vertex \,Cover| = |Maximum \,Bipartite \,Matching|\]따라서 최소 버텍스 커버를 찾고 싶으면 최대 이분 매칭을 하면 알 수 있다.
참고
최대 독립 집합 (Maximum Independent Set)
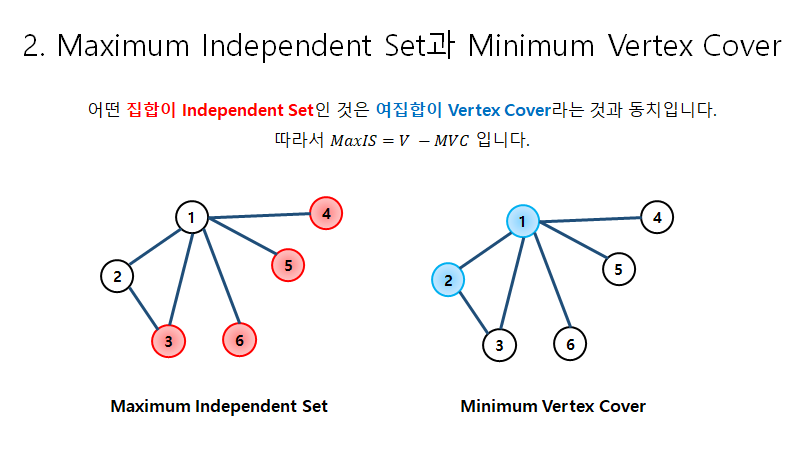 (최대 독립 집합)은 (최소 버텍스 커버)의 여집합이다.
(최대 독립 집합)은 (최소 버텍스 커버)의 여집합이다.
생각해보면 위 명제는 당연하다.
최소 버텍스 커버가 모든 edge의 한 쪽을 담당하고 있으니 나머지 노드를 모아보면 서로 인접할 수가 없다.

Leave a comment